Implement Simple Convolution with Java

In this post we are going to walk through the details and intuition behind simple convolution operation as one one of the most fundamental concept in Computer Vision. Additionally we will build a Java Application GUI which uses different convolution filters(implemented purely in java) to transform images of your choice. Please find the free open source code at this github repository as part of Packt Java Machine Learning for Computer Vision Course.

Table of Contents

How Computers perceive images

Although computers cannot perceive colors as we do they understand numbers quite good. So to no surprise a way was found to encode colors as numbers so a computer will understand.

For black an white(gray scale) images this is quite easy each number represent light intensity from 0 -255. With 0 meaning no light(black) and 255 meaning white so full brightness. Since in the end this numbers will be converted to colors in a display we need a number per display pixel. Pixels are two dimensional matrices with dimension like 1920 x 1080 or 1280 x 1024 therefore we will a number representing the light intensity per each of the matrices cell.

For colored images the idea stays the same but in addition we have three intensity of colors to take care Red, Green and Blue intensity(yes the famous RGB). So basically we need three of the two dimensional matrices we saw in white black case with each of them representing respective color intensity Red, Green and Blue(RGB). In a few words we will have a three dimensional matrix containing numbers from 0-255 representing intensity for one of the colors R,G,B e.x image[i][j][0] is Red value, image[i][j][1] Green value, image[i][j][2] Blue .

Edge Detection

Wikipedia definition : Edge detection includes a variety of mathematical methods that aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities.

The points at which image brightness changes sharply are typically organized into a set of curved line segments called edges.

Historically computer vision has always been a hard problem to solve due to small image data sets and because the problem is kind of hard in itself(you have a bunch of numbers and want to figure out what are those numbers representing). So for this reasons people had to come up with different techniques and methods to overcome this problem. Edge detection is one of those techniques that helped Computer Vision to achieve outstanding results and was first used for digit recognition back in 90’s(LeNet).

Relying completely on original images has proven to produce poor results because the model tends to be very sensitive to simple changes in light,shadows, not centered objects(object moving slightly left,right,down or up) etc… Edge Detection greatly helps with this problems because it enables the neural network to focus more on the object shapes(light intensity and object moving is not a big problem anymore) therefore make the prediction more robust.

Convolution

Although by now is clear that Edge Detection is worth to try we still need a way to implement it in a computer system where colors are matrices with numbers.

Vertical edge detection

Lets introduce a small matrix 3×3 called a filter more specifically a vertical filter.

1	0	-1
1	0	-1
1	0	-1

Additionally we are going to introduce an operation * called convolution and than simply convolve the image matrix(which is a simple black and white image on the left) with the vertical filter.

For the sake of the argument we are not using 0 for black but rather small number 10(not perfect black but very near).

The convolution operation will look like below:

We are just sliding the filter one position horizontally and vertically until the end. Each time we multiply the filter matrices elements with the selected area(sub-matrix) on the image matrix elements and than add all together. So for position (0,0) we do:

(1 * 255 + 0 * 255 + -1 * 255 )+ (1 * 255 + 0 * 255 + -1 * 255) +( 1 * 255 + 0 * 255 + -1 * 255) =0

while for position (0,1) we do:

(1 * 255 + 0 * 255 + -1 * 10 )+ (1 * 255 + 0 * 255 + -1 * 10) +( 1 * 255 + 0 * 255 + -1 * 10) =735

and son…

Eventually this will produce the below output matrix:

Lets analyse a bit what happened during the convolution.

First lets remind that we want to detect vertical edges and looking at the input image the edge is right into the middle. So the region where the color sharply changes from one color(white) to another(black).
It is easy to notice that right into the middle we have two rows of 735 values. Since the maximum number value we can have to represent a color is 255 for values bigger than that(735) we just don’t care but instead consider the maximum which 255. Same for values(e.x -735) less the than the minimum 0 we are going to consider 0 and ignore the rest. Following this approach the output matrix is visualized as an image with the sides as black and in the middle a white region.
Actually the white region on the output image is exactly the vertical edge we were looking for. So 735 values(white) were actually pointing out the presence on an edge while zeros(black) the absence of such edge. Indeed if look the input images on the sides(only white, only black ) there is no edges but rather only in the middle we have the color sharply changing from white to black.
Due to small images/matrix used for explanation reasons please notice that the white region is quite big making it hard to look like an edge. Anyway executed in the java application GUI on a bigger black and white image of 466 X 291 the results would look more clear like below e.x:

Horizontal edge detection

Horizontal edge detection is quite similar like the vertical one but is just using a different filter(flipped version of vertical filter).

Similarly notice how we have the 735 values right into the middle where the edge is located and zero values where there is no edge on the up and down sides. Executed in the java application GUI on a bigger black and white image of 466 X 291 the results would look more clear like below e.x:

Other Edge Detectors

There also other edge detectors beside what we saw so fare and we will see them all in action when running the java edge detection application.

Sobel and Scharr can also flipped and transform to horizontal version. Both of them introduce more weights on the sides by making the edge thicker(more on show case).

Edge Detection Intuition

By now we already have an intuition why convolution detect edges so lets shortly re visit what happened.

In the figure above we have the vertical filter on red and the horizontal filter green. Regardless of their position on the matrix the filters are both interested on sides by ignoring the middle row. Filters are interested if there is any difference in numbers(recall numbers are colors so change in color so edge) on the sides by ignoring the middle. Depending on the sides values their could be two cases:

When both sides have the same values the sum will be zero since the middle is ignored and filter have positive and negative values on sides. This simply means there is not edge on this region selected by the filter.
When both sides are different the sum will have a value different than zero (usually in absolute terms big)since the middle is ignored and filter have positive and negative values on sides. As we saw previously big values indicate the presence of an edge since the color on the sides has sharply changed.

Convolution on Colored Images

As we know RGB images differ from black and white by having instead of one three matrices with values from 0-255 each representing intensity of Red,Green and Blue color. So as you may already figure it out by now it looks reasonable to convolve each of this matrices with some chosen filter(not necessarily the same filter as in figure).

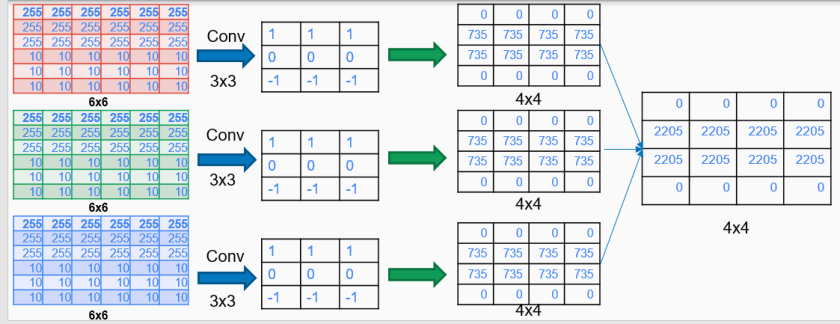Convolving with three filters each will result in three output matrices each representing the convolution output of specific color(R,G,B). Having a closer look a this matrices we will notice that actually those matrices are not representing anymore colors but rather represent the presence of an edge or not. So each those pixels(matrices cells) not are flagging the possibility of an edge presence. Therefore keeping them separated does not bring any value since there is no RGB anymore. As a result we are going to sum all three those matrices together and have only one matrices as result.

Convolution in Neural Networks

Although so fare we have seen different type of filters or convolution types, there is still one question: what filter or convolution works better with neural networks for specific problem?

As we already mention computer vision problems are hard and is quite difficult and in flexible to choose only one of the filters or even a mixture of them. So why don’t we let the neural networks figure out what type of filters works better for a particular problem?

Maybe Neural Networks can find out better filters than Vertical,Horizontal or Sobel. So instead of having filters with values on the matrices cells we are going to parametrize(W^ij) those cells and let the neural network learn those parameters as it needs.

The purpose of this post is to walk through the intuition of convolution and implement a simple convolution in pure java. When it comes in using the convolution in deep neural networks there are a few more details related to convolution which are explained in detail in previous post as Convolution Parameters , Pooling Layers and in addition also a java application for hand wiring digits recognition is build using the explained concepts(for more application about deep convolution networks please refer at CatVsDog Recognition Java Application).

The Code

The details of the full code can be found at this github repository as part of Packt Java Machine Learning for Computer Vision course.

As a first step we will need to read a colored RGB images and build a three dimensional matrix out of that:

private double[][][] transformImageToArray(BufferedImage bufferedImage) {
    int width = bufferedImage.getWidth();
    int height = bufferedImage.getHeight();

    double[][][] image = new double[3][height][width];
    for (int i = 0; i < height; i++) {
        for (int j = 0; j < width; j++) {
            Color color = new Color(bufferedImage.getRGB(j, i));
            image[0][i][j] = color.getRed();
            image[1][i][j] = color.getGreen();
            image[2][i][j] = color.getBlue();
        }
    }
    return image;
}

Than as we saw during the theory we need to apply convolution with some chosen filter to each of this matrices R,G,B and of course in the end we will sum up since convolution on colored images produces on matrix:

private double[][] applyConvolution(int width, int height, double[][][] image, double[][] filter) {
    Convolution convolution = new Convolution();
    double[][] redConv = convolution.convolutionType2(image[0], height, width, filter, 3, 3, 1);
    double[][] greenConv = convolution.convolutionType2(image[1], height, width, filter, 3, 3, 1);
    double[][] blueConv = convolution.convolutionType2(image[2], height, width, filter, 3, 3, 1);
    double[][] finalConv = new double[redConv.length][redConv[0].length];
//sum up all convolution outputs
    for (int i = 0; i < redConv.length; i++) {
        for (int j = 0; j < redConv[i].length; j++) {
            finalConv[i][j] = redConv[i][j] + greenConv[i][j] + blueConv[i][j];
        }
    }
    return finalConv;
}

After that there is one last step is showing the convolution output matrix as an image into GUI:

private File createImageFromConvolutionMatrix(BufferedImage originalImage, double[][] imageRGB) throws IOException {
    BufferedImage writeBackImage = new BufferedImage(originalImage.getWidth(), originalImage.getHeight(), BufferedImage.TYPE_INT_RGB);
    for (int i = 0; i < imageRGB.length; i++) {
        for (int j = 0; j < imageRGB[i].length; j++) {
            Color color = new Color(fixOutOfRangeRGBValues(imageRGB[i][j]),
                    fixOutOfRangeRGBValues(imageRGB[i][j]),
                    fixOutOfRangeRGBValues(imageRGB[i][j]));
            writeBackImage.setRGB(j, i, color.getRGB());
        }
    }
    File outputFile = new File("EdgeDetection/edgesTmp.png");
    ImageIO.write(writeBackImage, "png", outputFile);
    return outputFile;
}

private int fixOutOfRangeRGBValues(double value) {
    if (value < 0.0) {
        value = -value;
    }
    if (value > 255) {
        return 255;
    } else {
        return (int) value;
    }
}

As we already mention values bigger than 255 are just 255 and values smaller than 0 are just 0 because there is the only way we can show the image in java in RGB(probably other languages as well).

In the end we need to put all together with below simple method:

public File detectEdges(BufferedImage bufferedImage, String selectedFilter) throws IOException {
    double[][][] image = transformImageToArray(bufferedImage);
    double[][] filter = filterMap.get(selectedFilter);
    double[][] convolvedPixels = applyConvolution(bufferedImage.getWidth(),
            bufferedImage.getHeight(), image, filter);
    return createImageFromConvolutionMatrix(bufferedImage, convolvedPixels);
}

Of course there is one last piece missing the convolution operation itself. The code is a bit too long(less than 140 lines) to show full in here but quite straight forward so please feel free to explore Convolution class in github.

public double[][] convolutionType2(double[][] input,
                                   int width, int height,
                                   double[][] kernel,
                                   int kernelWidth, int kernelHeight,
                                   int iterations) {
    double[][] newInput = input.clone();
    double[][] output = input.clone();

    for (int i = 0; i < iterations; ++i) {
        output = convolution2DPadded(newInput, width, height,
                kernel, kernelWidth, kernelHeight);
        newInput = output.clone();
    }
    return output;
}

Application & Showcase

Application can be run by executing RunEdgeDetection class and than GUI will be shown as below in which a type of filter is chosen together with an images: